本五主要介绍NTC热敏电阻计算公式。Steinhart-Hart方程是计算NTC热敏电阻的主要数学模型,它适合于高精度的宽温度范围。提供了基于给定热敏电阻的温度阻抗表计算特征Steinhart-Hart系数的软件,以及允许将温度值转换为电阻的功能,反之亦然。
1:说明
Steinhart和Hart 1968([1])发现了半导体电阻率随温度变化的模型。Steinhart-Hart定律将绝对温度T(单位为开尔文)描述为NTC热敏电阻的电阻率(Ω)的函数,根据公式
|
1 / T = a 0 + a 1 ·ln r + a 3 ·(ln r)3
|
下图显示了NTC热敏电阻特性的典型图形,给出了电阻的自然对数(以Ω为单位)的倒数温度(单位为K)。
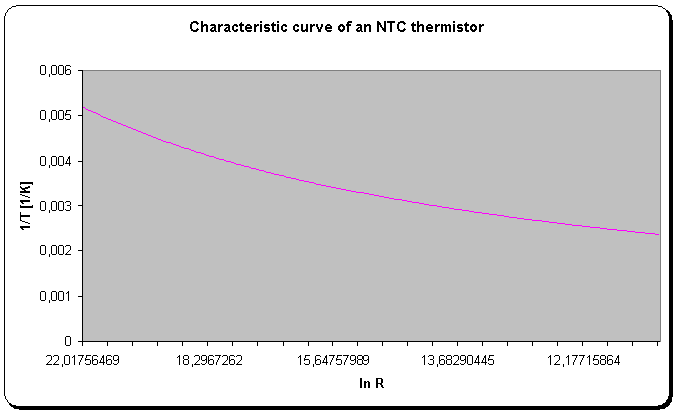
常数a 0,a 1和a 3(也称为Steinhart-Hart系数)根据热敏电阻的类型而变化。为了支持开发人员在创建温度测量应用时,热敏电阻制造商经常为他们的产品提供这些常数。他们还公布表格,其中列出了温度范围更广的热敏电阻产品的电阻率。
这个项目提供了软件
- 用给定的Steinhart-Hart系数计算给定电阻的NTC热敏电阻的温度值,
- 用给定的斯坦哈特 - 哈特(Steinhart-Hart)系数计算给定温度下NTC热敏电阻的电阻值
- 评估由耐温表描述的NTC热敏电阻的Steinhart-Hart系数。
除了标准Steinhart-Hart方程之外,其他形式也被发现。对于较低CPU功率的应用,可以使用Steinhart-Hart方程的简化形式。
|
1 / T = a 0 + a 1 ·ln r
|
另一方面,可以在公式中插入一个二次项来提高扩展Steinhart-Hart方程的精度
|
1 / T = a 0 + a 1 ·ln r + a 2 ·(ln r)2+ a 3 ·(ln r)3
|
2、软件
该项目提供了软件,用于在算法中给出的计算。类/模块可以用于
- 从电阻转换为温度,
- 从温度转换为电阻,
- 计算NTC热敏电阻的Steinhart-Hart系数,其特性为TR表。
后者可以用于标准,简化或扩展的Steinhart-Hart多项式。
2.1 Java类
对于Java,以下类可用
| 类 | 描述 |
|---|---|
| NtcException | 在这个热敏电阻框架中使用的例外 |
| NtcTable |
代表NTC热敏电阻的TR表。 |
| NtcThermistorModel |
表示使用Steinhart-Hart多项式1 / T = a 0 + a 1 ·ln r + a 3 ·(ln r)3建模的NTC热敏电阻。 模型将使用NtcTable对象创建。它提供了读取热敏电阻名称的方法,获得NtcTable对象,获得Steinhart-Hart系数以及从温度转换为电阻的方法,反之亦然。 |
| NtcThermistorExtendedModel |
表示使用扩展Steinhart-Hart多项式1 / T = a 0 + a 1 ·ln r + a 2 ·(ln r)2 + a 3 ·(ln r)3建模的NTC热敏电阻。 |
| NtcThermistorSimplifiedModel |
表示使用简化的Steinhart-Hart多项式1 / T = a 0 + a 1 ·ln r建模的NTC热敏电阻。 源自NtcThermistorModel,提供了相同的方法。 |
注意:项目中使用了泛型,因此需要Java 5或更高版本。
一个小的测试类NtcTest是包的一部分,包含一个包含理论NTC(simu.txt)的TR表的示例文本文件。为了使开发者生活变得简单,整个应用程序被部署为一个(可执行的)jar文件,其中包含所有的源代码,类和主类为NtcTest的清单文件。
下载测试应用程序后可以调用
java -jar thermistor.0.1.jar
2.2 C模块
有三个C模块可用
| 模 | 描述 |
|---|---|
| coeff.c | 用于从NTC表(用文本文件给出)计算Steinhart-Hart系数的程序。 |
| ttor.c |
Ť emperature 到 ř esistance计算。 |
| rtot.c | ř esistance 到 吨 emperature计算。 |
对于在Windows下的使用,它们已经被编译(使用Cygwin的C编译器)。对于其他操作系统,请使用您的系统C编译器进行编译。包含理论上NTC(simu.txt)的TR表格的示例文本文件也被提供用于测试目的。
3、算法
3.1从电阻转换到温度
基于NTC热敏电阻的测量电阻值,扩展Steinhart-Hart方程允许简单计算温度
1 / T = a 0 + a 1 ·ln r + a 2 ·(ln r)2 + a 3 ·(ln r)3
这里r是Ω中的电阻,T是K中的绝对温度(K =开尔文)。在绝对零T abs = -273.15℃的情况下,以℃ 为单位的温度t的公式最终导致
t = 273,15℃+ [ a 0 + a 1 ·ln r + a 2 ·(ln r)2 + a 3 ·(ln r)3 ] -1
通过将适当的系数设置为零,可以按照简化或标准Steinhart-Hart方程进行计算。
3.2从温度转换为电阻
在Ω从温度以℃计算电阻值根ř扩展斯坦哈特-Hart公式的,必须找到(为简单地设定的标准多项式一个2 = 0在下面的公式)
1 / T = a 0 + a 1 ·ln r + a 2 ·(ln r)2 + a 3 ·(ln r)3
与Y = LN [R ,我们得到
1 / T = a 0 + a 1 ·y + a 2 ·y 2 + a 3 ·y 3
我们介绍替换
T = t + T abs
b = a 2 / a 3
c = a 1 / a 3
d =(a 0 -1 / T)/ a 3
p = c - ⅓·b 2
q = 2 / 27 · b 3 - 1 / 3 · b · c + d
U = [-q / 2 +(Q 2 /4 + p 3 /27)½ ] ⅓
V = [-q / 2 - (Q 2 /4 + p 3 /27)½ ] ⅓
得到
r = e u + v - b / 3
对于给定温度t(以°C为单位)的电阻r(以Ω为单位)。
3.3 Steinhart-Hart系数的计算
有时使用特殊的温度值来计算系数。在感兴趣的范围内插入四个数值对到扩展Steinhart-Hart poylonm中,得到一个线性代数方程组(标准Steinhart-Hart多项式的三个值对)。通常使用的温度是例如0℃,15℃,25℃和70℃下通过求解该系统中的值,一个0,一个1,一个2和一个3可以被确定。
更好的方法是在1801年由卡尔·弗里德里希·高斯(Carl FriederichGauß)引入的称为普通最小二乘(OLS)的数学优化技术。有关OLS理论的详细信息在Wikipedia [ 3 ]或MathPlanet [ 4 ]中给出。
如果近似的函数是一个多项式,则向量空间,标量乘积和正交基的理论便于计算。给出一个n个耐温对的列表
(r 0, t 0),(r 1, t 1),...,(r n-1, t n-1)
(其中n应该至少为3),Steinhart-Hart系数的最佳拟合问题导致最小化
| n-1个 | ||
| sum:= | Σ | [t(r i)-t i ] 2 |
| I = 0 |
其中t i是第i个温度值,t(r i)是根据该多项式计算的温度。
这个优化需要一个小的数学偏移。为正整数Ñ和横坐标值给出X 0,X 1,...,X N-1与度≤的polynoms Ñ建立一个向量空间V。在V上可以定义一个标量积
| ñ | ||
| [p,q]:= | Σ | p(x i)·q(x i) |
| I = 0 |
通过
标量产品使V成为规范空间。对于具有纵坐标值的函数f
y i:= f(x i)
对于i = 0,...,N-1恰好有一个多项式p ˚F在V相匹配中的坐标的函数(X 0,ÿ 0), (X 1,ÿ 1),..., (X Ñ -1,y n-1)。
如果poisitve整数米, 与米≤ N,给出的所有度polynms ≤ 米建立的子空间ü的V。由U中的多项式对f的最佳近似的问题相当于由U中的多项式对p f的最佳近似,|。
| n-1个 | n-1个 | ||||||
| s = | Σ | [u f(x i)-y i ]² | = | Σ | [u f(x i)-p f(x i)] 2 | = | | u f -p f | |
| I = 0 | I = 0 |
回答问题的最后结果是很容易的,如果一个标准正交基【U 1,U 2,...,U 中号 }的ü给出。对于p ˚F最佳逼近ü ˚F 作为计算
| 米 | ||
| u f = | Σ | [u 我,p f ]·u 我 |
| I = 1 |
例如,如果给定一个RT表,其值为从0°C到100°C,步长为1°C,则多项式p f的次数为101(!)。幸运的是一定不会被发现,为了找到斯坦哈特-哈特coefficicents,从而找到ü ˚F。从U的规范基{V 1 = 1,V 2 = X,V 3 = X 2,V 4 = X 3}开始,可以评价正交基{U 1,U 2,U 3,U 4 }。之后,u f的系数由上述总和计算。
该坐标
(x 0,y 0),(x 1,y 1),...,(x n-1,y n-1)
从温度 - 电阻对计算得出
x i = ln r i
y i = 1 /(t i -T abs)
对于i = 0,...,n-1。
正交基 的ü被递归地进行评价。我们设置
u 1 = v 1 = 1
和
| I-1 | ||
| w i = v i - | Σ | [ü Ĵ,U ]·U |
| J = 1 |
ü = W / | W | 1/2
对于i = 2,...,m = 4。
有了这个基础,我们可以计算出ü ˚F为
| m | ||
| u f = | Σ | [u ,p f ]·u |
| I = 1 |
并根据该方程确定Steinhart-Hart系数。(请注意,标量积可以在不知道被计算p ˚F如上所述)。






